Gaussian elimination
We can solve linear equation systems, or matrices of the form:
Ax=B
Or,
![[a_(11) a_(12) ... a_(1k); a_(21) a_(22) ... a_(2k); | | ... |; a_(k1) a_(k2) ... a_(kk)][x_1; x_2; |; x_k]=[b_1; b_2; |; b_k],](http://mathworld.wolfram.com/images/equations/GaussianElimination/NumberedEquation2.gif) |
If you want you can use the matrix in extended form:
![[a_(11) a_(12) ... a_(1k); a_(21) a_(22) ... a_(2k); | | ... |; a_(k1) a_(k2) ... a_(kk)|b_1; b_2; |; b_k][x_1; x_2; |; x_k].](http://mathworld.wolfram.com/images/equations/GaussianElimination/NumberedEquation3.gif) |
You have to use elementary row operations till the matrix will be an upper triangular, like this:
![[a_(11)^' a_(12)^' ... a_(1k)^'; 0 a_(22)^' ... a_(2k)^'; | | ... |; 0 0 ... a_(kk)^'|b_1^'; b_2^'; |; b_k^'].](http://mathworld.wolfram.com/images/equations/GaussianElimination/NumberedEquation4.gif) |
At this moment we can solve the first unknown value, and using following expression we can obtain all of them:
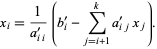
For instance, we have following linear equations system:
Lets write it like a matrix:
Applying Gaussian Elimination we have:
Its a upper triangular matrix, here we know that:
Z = 2
Going back we can obtain X and Y values, because:
Y - 5Z = -9
Solving for Y:
Y=1
Next step is find X:
X + Y + 2Z = 8
where,
X=3



Source: http://mathworld.wolfram.com/GaussianElimination.html
ResponderEliminarhttp://www.cs.caltech.edu/courses/cs171/c2-1.pdf
ResponderEliminar